Recently, I decided to dive into the fundamentals of machine learning algorithms in a structured way, aiming to avoid superficial understanding. To deepen my knowledge, I plan to implement basic machine learning algorithms on my own. This article is the first in a series where I will walk through the implementation of a Decision Tree algorithm. In this post, I’ll summarize the key concepts behind decision trees and provide my own code implementation. All the code and training data for the models are available on GitHub, so you can follow along and experiment yourself.
In this article, I will build a decision tree step by step using the contact lens prescription dataset from MLiA (Machine Learning in Action). I will also visualize the resulting decision tree using Graphviz, which helps in better understanding the structure of the model.
Decision Tree Learning
Decision tree learning is a type of supervised learning method that uses a tree-like model of decisions and their possible consequences. It can be used for both classification and regression tasks. Common algorithms include ID3, C4.5, and CART. The process of building a decision tree involves selecting the best attribute to split the data, aiming to create the most homogeneous subsets. This process is essentially how the model learns patterns from the data.
Decision Tree Structure
A simple example of a decision tree could be one that predicts whether a person should buy a computer based on certain attributes. Internal nodes represent features or attributes, branches represent the possible values of those features, and leaf nodes represent the final decision or outcome.
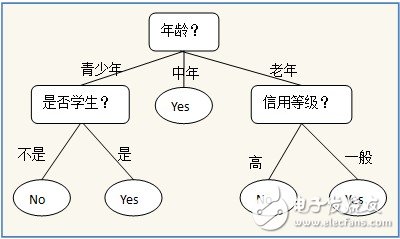
Visualization tools like Graphviz or matplotlib annotations can help us understand the structure of the decision tree more intuitively. Unlike some other models such as neural networks or Bayesian classifiers, decision trees offer a clear and interpretable representation of the decision-making process.
Decision Tree Algorithms
The core of a decision tree algorithm lies in selecting the optimal feature for splitting the data. The goal is to find the feature that best separates the data into distinct classes, making the subsets as "pure" as possible. The underlying principle is to reduce disorder or uncertainty in the data.
There are several methods for selecting the best feature:
- Information Gain
- Gain Ratio
- Gini Impurity
Information Gain
Information gain is based on the concept of entropy from information theory. Entropy measures the impurity or uncertainty in a set of examples. The lower the entropy, the more "pure" the subset. Here’s a brief overview of the key concepts:
- The amount of information in an event is defined as the negative logarithm of its probability.
- Information entropy is the average amount of information in a set of events, calculated as the expected value of the information content.

Using Python, we can calculate the Shannon entropy of a dataset by counting the frequency of each class and applying the entropy formula. Here's a sample implementation:
def get_shanno_entropy(self, values):
'''Calculate the Shanno Entropy based on the given list of values'''
unique_vals = set(values)
val_counts = {key: values.count(key) for key in unique_vals}
probs = [v / len(values) for k, v in val_counts.items()]
entropy = sum([-prob * log2(prob) for prob in probs])
return entropy
Once we have the entropy, we can evaluate the information gain after splitting the dataset. Information gain is the difference between the entropy before and after the split. This helps determine which feature provides the most useful information for classification.
Here’s a snippet of the code used to select the best feature based on information gain:
def choose_best_split_feature(self, dataset, classes):
'''Determine the feature that provides the best split based on information gain'''
base_entropy = self.get_shanno_entropy(classes)
feat_num = len(dataset[0])
entropy_gains = []
for i in range(feat_num):
splited_dict = self.split_dataset(dataset, classes, i)
new_entropy = sum([
len(sub_classes) / len(classes) * self.get_shanno_entropy(sub_classes)
for _, (_, sub_classes) in splited_dict.items()
])
entropy_gains.append(base_entropy - new_entropy)
return entropy_gains.index(max(entropy_gains))
Although I initially misunderstood the concept of information gain, this helped me refine my code and improve the accuracy of the decision tree. Moving forward, I’ll explore other criteria like the gain ratio and Gini impurity to further enhance the model.
Shenzhen Ousida Technology Co., Ltd , https://en.osdvape.com