Decision tree construction and visualization of decision trees using Graphviz

Recently, I decided to take a more structured approach to learning the fundamental algorithms of machine learning. Instead of relying on vague understanding or shortcuts, I chose to implement core machine learning algorithms myself to deepen my comprehension. This article is the first in a series where I will walk through the implementation of various machine learning models. Specifically, this post focuses on decision trees, summarizing the key algorithms and providing my own code implementation. All the code and training data are available on GitHub for reference.

In this article, I will build a decision tree step by step using the contact lens prescription dataset from MLiA (Machine Learning in Action), and visualize the resulting tree using Graphviz. This hands-on approach will help me better understand how decision trees work and how they can be used to make predictions based on data attributes.

Decision Tree Learning

Decision tree learning is a method that uses a tree structure to represent decisions based on data attributes. It's widely used for both classification and regression tasks. Popular algorithms include ID3, C4.5, and CART. The process of building a decision tree involves extracting knowledge from the data and transforming it into a set of rules. This rule-based structure is what makes the tree a powerful tool for machine learning.

Decision Tree Structure

A decision tree consists of internal nodes that represent features, branches that represent possible values of those features, and leaf nodes that indicate the final decision or outcome. For example, a simple decision tree might predict whether someone should buy a computer based on factors like age, income, and student status.

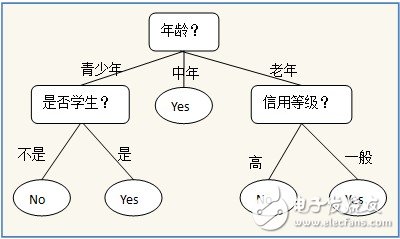
Visualization tools such as Graphviz or matplotlib annotations allow us to see the structure of the tree we've built. This visual representation helps in interpreting the model and understanding how it makes decisions—something that isn't as intuitive in models like neural networks or Bayesian classifiers.

Decision Tree Algorithms

At the heart of any decision tree is the algorithm used to select the best feature for splitting the data. The goal is to choose the attribute that maximizes the purity of the resulting subsets. This process transforms unordered data into a more structured form, making it easier to draw conclusions.

There are several common methods for selecting the best feature:

1. Information Gain
2. Gain Ratio
3. Gini Impurity

Information Gain

Information gain is one of the most commonly used criteria in decision tree algorithms. It relies on concepts from information theory, such as entropy and information content. The basic idea is that an event with a higher probability contributes less information than one with a lower probability.

The amount of information associated with an event is defined as the negative logarithm of its probability. Entropy, on the other hand, measures the average amount of information in a dataset. The formula for entropy is:

Using Python, we can calculate the entropy of a dataset by counting the frequency of each class and applying the formula. Here’s a sample implementation:

def get_shanno_entropy(self, values):
    '''
    Calculate the Shanno Entropy based on the values in the given list
    '''
    unique_vals = set(values)
    val_nums = {key: values.count(key) for key in unique_vals}
    probs = [v / len(values) for k, v in val_nums.items()]
    entropy = sum([-prob * log2(prob) for prob in probs])
    return entropy

Once we have the entropy of the original dataset, we can split the data based on different features and calculate the new entropy for each subset. The difference between the original entropy and the weighted average of the new entropies gives us the information gain. The feature with the highest information gain is selected for splitting the tree.

My initial implementation had some issues, which led to incorrect tree structures. After debugging, I was able to refine the algorithm to correctly identify the best feature for splitting at each node.

Gain Ratio

While information gain is effective, it tends to favor features with a large number of distinct values. To address this, the gain ratio was introduced. It adjusts the information gain by dividing it by the intrinsic information of the feature, which accounts for the number of splits the feature creates. This helps prevent overfitting and ensures a more balanced tree structure.

Breeze Pro Vape 2000Puffs

 It all begins with the Breeze Pro's new elegant design. Premium materials encompassed by a beautifully designed shell helps this Disposable Vape really stand out. Inside, you'll find a powerful 1,000mAh battery capable of 2,000 puffs, 6mL of 5% salt nicotine vape juice, and a new and enhanced mesh coil design. It's this detailed engineering which has propelled Breeze Smoke as one of the best disposable vape manufacturers on the market. Once again with the Breeze Pro, they've hit a home run.

Breeze pro vape 2000Puffs.Breeze Pro.Breeze vape,Breeze Pro disposable vape ,Breeze vape pen

Shenzhen Ousida Technology Co., Ltd , https://en.osdvape.com